Até meados do século XIX, os conceitos de magnetismo, eletricidade, luz e radiação associada eram tratados separadamente. Em 1864, o físico James Clerk Maxwell trabalhou na unificação dessas teorias e fenômenos: as Leis de Gauss para a campos elétricos e magnéticos, a Lei de Faraday para a indução eletromagnética e a Lei de Ampère que relaciona campo magnético e corrente elétrica.
As equações fornecem um modelo matemático para tecnologias elétricas, ópticas e de rádio, como geração de energia, motores elétricos, comunicação sem fio, lentes, radar, etc. Elas descrevem como os campos elétricos e magnéticos são gerados por cargas, correntes e mudanças nesses campos. Essas equações diferenciais também foram protagonistas na primeira definição real de que a luz é uma onda eletromagnética e sua velocidade é de 299.792.458 metros por segundo.
As equações de Maxwell para o eletromagnetismo são surpreendentemente visuais e relativamente simples para tamanha importância. Não se assuste, estou apenas as demonstrando. Até o final dessa matéria você entenderá o que elas significam.
São elas:
$$\nabla \cdot \vec{E} = \frac{\rho}{\varepsilon_0}$$
$$\nabla \times \vec{E} = – \frac{\partial \vec{B}}{\partial t}$$
$$\nabla \cdot \vec{B} = 0$$
$$\nabla \times \vec{B} = \mu _0 \vec{J} + \mu _0 \varepsilon _{0}{\frac {\partial \vec{E}}{\partial t}}$$
A primeira equação se chama Lei de Gauss e descreve as linhas de campo elétrico, começando nas partículas positivas e terminando nas partículas negativas. A segunda equação é a Lei de Faraday, descrevendo que a variação de um campo magnético produz um campo elétrico. A terceira equação é a Lei de Gauss para o magnetismo, que descreve que é impossível existir um monopolo magnético. E a quarta equação é a Lei de Ampère-Maxwell, que diz que uma corrente elétrica ou uma variação do fluxo elétrico (ou ambos) geram um campo magnético.
Antes de continuar…
Na Física usamos muito a palavra campo. Quando falamos em campo gravitacional, o que você imagina? Uma região do espaço onde a gravidade é atuante, como em volta de um planeta, estrela ou buraco negro. Com o campo elétrico e campo magnético é exatamente mesma coisa. Um campo magnético significa uma região do espaço capaz de exercer força em materiais com propriedades magnéticas, por exemplo.
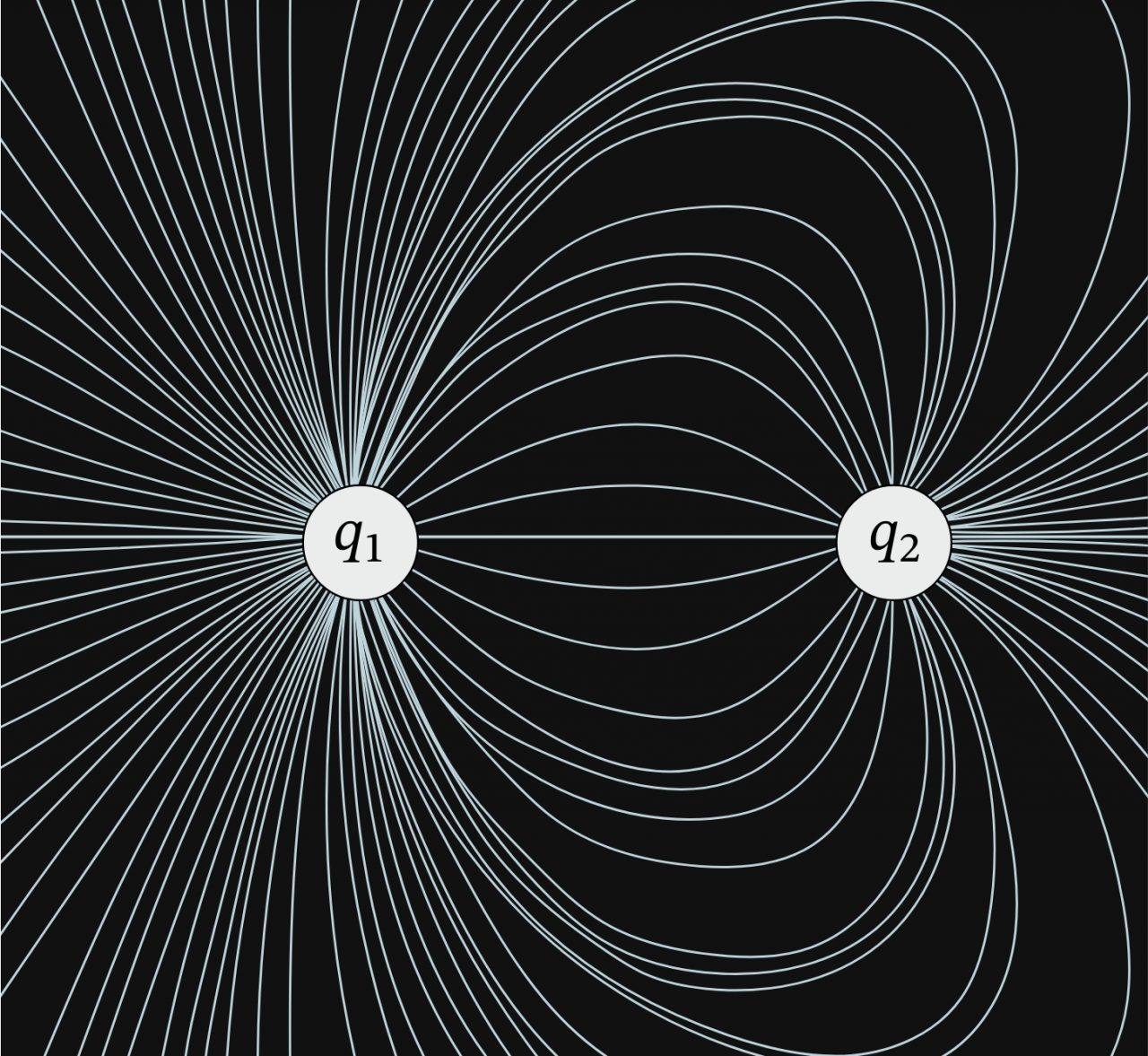
E para representar esses campos usamos linhas (como a imagem que ilustra a capa dessa matéria). Essas linhas são chamadas de, naturalmente, linhas de campo ou linhas de força. Elas possuem pequenas setas para indicar o sentido do fluxo desse campo (fique atento a elas) e a quantidade de linhas indica a intensidade desse campo.
Importante mencionar também as setinhas em cima das letras, como $\vec{E}$ e $\vec{B}$. Isso indica que são vetores, e vetores indicam uma grandeza que possui intensidade, direção e sentido (um campo magnético tem direção, tem sentido e tem intensidade, certo?).
Sopa de letrinhas, socorro!
Antes de continuar, é muito importante saber o que cada letra nessas equações significa. Acredite, as explicações lá na frente ficarão mais fáceis. Vamos começar pelas letronas do lado esquerdo das equações (que tem a setinha em cima, indicando que se trata de um vetor).
- $\vec{E}$: campo elétrico
- $\vec{B}$: campo magnético
- $\vec{J}$: densidade da corrente elétrica
É só isso. Se do lado esquerdo da equação você ver um $\vec{E}$ significa que aquela equação está tratando de alguma alteração do campo elétrico. O mesmo serve para o $\vec{B}$ sobre o campo magnético. Por que campo magnético usa a letra B? Não tem nenhuma lógica por trás, James Maxwell simplesmente nomeou os campos em ordem alfabética, A, B, C, D, até a letra H, e a letra B ficou para o campo magnético. O $\vec{B}$ pegou e tornou uma convenção na Física.
Vamos para o próximo símbolo misterioso:
- $\frac{\partial}{\partial t}$ ou $\frac{d}{dt}$: derivada em função do tempo
Isso parece bem difícil, mas prometo que não é. Em matemática, uma derivada é simplesmente uma taxa de variação. Por exemplo, se você está viajando num carro a 80 km/h significa que em 1 hora você estará a 80 km de distância; depois de 2 horas estará a 160 km de distância. Como medimos essa taxa de variação? Com a velocidade! Ou seja, a taxa de variação de uma distância $x$ em função de um tempo $t$ é a velocidade $v$, ou matematicamente: $v = \frac{dx}{dt}$.
Vamos continuar:
- $\mu_0$: constante magnética, é um número fixo (1,2566×10-6 H/m)
- $\varepsilon_0$: constante elétrica, também um número fixo (8,854187×10-12 F/m)
Essas letras gregas são os símbolos mais fáceis. São constantes, ou seja, números fixos. Basta pegar esses números longos e substituir nas equações, e pronto. Está feito! Então vamos para a próxima leva:
- $\nabla \cdot$: divergência
- $\nabla \times$: rotacional
Talvez o conceito mais chatinho e exige mais imaginação. Esse símbolo de “triângulo invertido” (que se chama nabla) pode seguir acompanhado de um ponto ou um $\times$. Esse sinal que vem depois do nabla muda totalmente seu significado.
Vamos começar com a divergência ($\nabla \cdot$), que apresenta alguns conceitos prévios.
Imagine a superfície de uma pia de cozinha com a torneira aberta. O que acontece? A água bate em um ponto e se espalha para todos os lados. Agora imagine o ralo dessa mesma pia. O que acontece? A água toda se move na direção de um único ponto, o ralo. Isso é divergência! A divergência mede a intensidade de um escoamento para dentro ou para fora de uma região. Uma divergência positiva significa um fluxo para fora dessa região; uma divergência negativa significa um fluxo se concentrando num ponto de uma região. E a divergência zero? Significa apenas um fluxo onde a entrada e a saída são iguais, a quantidade de água que entra é igual à quantidade de água que sai (como um rio).
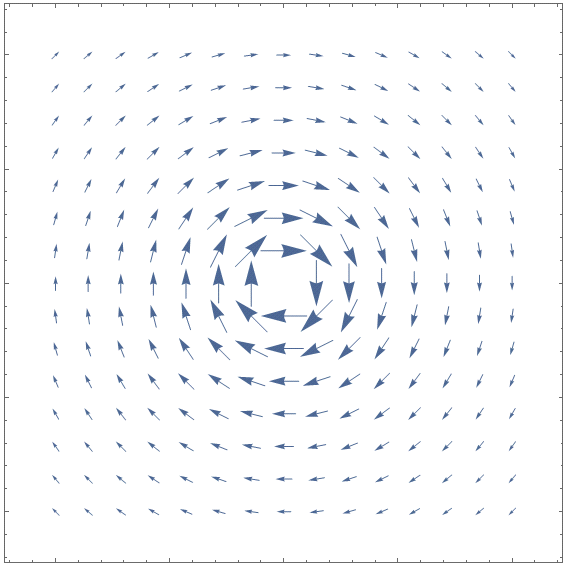
Mas e a rotacional ($\nabla \times$)?
Vamos manter nossos experimentos mentais: agora imagine um tornado lá no Texas. Todo o ar dentro do tornado está girando, se movimentando em redemoinhos. Isso são rotacionais! Quanto maior o valor da rotacional, mais intenso é esse redemoinho. No lado de fora do tornado o vento vai se acalmando cada vez mais, ou seja, o rotacional vai se aproximando de zero.
Agora, vamos falar sobre nosso último símbolo:
- $\rho$: densidade de carga elétrica
Essa letra grega se chama rô, e significa a quantidade total de carga elétrica. Quanto maior o número, maior a carga elétrica total. É basicamente um número qualquer que pode ser medido com um instrumento. Como uma carga elétrica pode ser positiva ou negativa, então esse número pode ser positivo ou negativo. Guarde bem isso!
Agora que sabemos o que significa cada símbolo matemático, vamos às fórmulas!
Lei de Gauss
Essa é a fórmula da Lei de Gauss:
$$\nabla \cdot \vec{E} = \frac{\rho}{\varepsilon_0}$$
Ela diz pra que sentido as linhas de campo se orientam com uma carga elétrica. As linhas de campo saem das partículas positivas e vão para as partículas negativas. Traduzindo para o português, podemos escrever essa equação como sendo:
$$\textrm{divergência do campo elétrico} = \frac{\textrm{carga elétrica}}{\textrm{constante elétrica}}$$
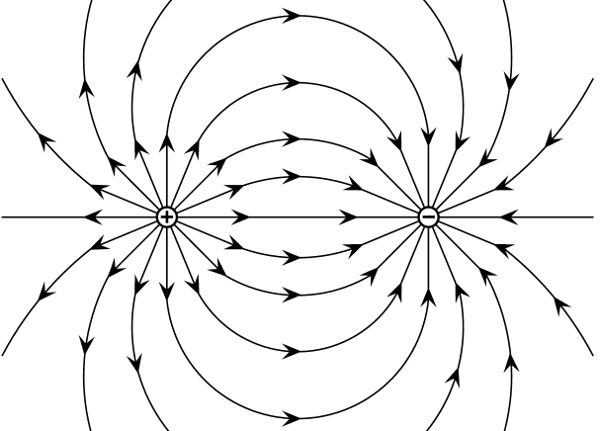
É exatamente isso que vemos na ilustração do campo elétrico ao lado! Se a carga de uma partícula for positiva, como um próton, então a divergência será positiva e as linhas de campo saem dessa partícula. Se a carga for negativa, como um elétron, a divergência também será negativa e as linhas de campo elétrico irão se concentrar nele!
Lindo, não é?
Lei de Faraday
A lei de Faraday descreve um fenômeno conhecido como indução eletromagnética. A equação tem alguns símbolos um pouco diferentes:
$$\nabla \times \vec{E} = – \frac{\partial \vec{B}}{\partial t}$$
Vamos traduzir ela para o português:
$$\textrm{rotacional do campo elétrico} = \textrm{variação do campo magnético}$$
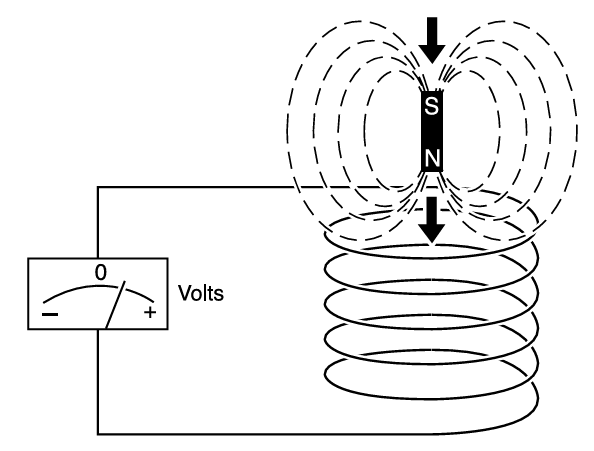
Observe o símbolo de campo magnético ($\vec{B}$) ali na taxa de variação ($\partial \vec{B}$). Ela diz que a taxa de variação de um campo magnético em um determinado tempo ($t$) produz um campo elétrico. Quanto mais intensa a taxa de variação, mais forte será a produção desse campo elétrico, ou seja, mais intensa será a corrente elétrica gerada.
Essa lei é fundamental, pois descreve de forma matemática como funciona algo que a humanidade é totalmente dependente: guitarras elétricas geradores elétricos. Dentro de um gerador temos ímãs conectados em um eixo que, quando gira, vão variando o campo magnético, produzindo eletricidade para abastecer as cidades do mundo inteiro.
OBS: apesar da piada, as guitarras elétricas também funcionam pelo mesmo princípio. A vibração das cordas faz variar o campo magnético do captador, transformando em eletricidade até o amplificador. 🙂
Lei de Gauss para o magnetismo
Essa lei tem uma fórmula bem fácil de entender caso você tenha captado bem a ideia do que é divergência:
$$\nabla \cdot \vec{B} = 0$$
Vamos lá, substituindo os símbolos por palavras no nosso idioma:
$$\textrm{divergência do campo magnético} = \textrm{zero}$$

Bem simples, não? Mas o que ela diz é que não existem monopolos magnéticos. Ao contrário do campo elétrico, não existe uma “carga magnética” positiva ou negativa. Uma superfície com um campo magnético tem sempre um polo norte e um polo sul formando um loop fechado. É o que chamamos de dipolo magnético.
Se você pegar um ímã e cortá-lo na metade, você terá dois ímãs, cada um contendo um polo norte e um polo sul. Ou seja, as linhas de campo magnético que saem no polo norte (fonte) retornam para o polo sul (dreno), formando uma espécie de círculo. A divergência total é zero.
Lei de Ampère-Maxwell
Essa equação é um pouquinho maior porque ela reúne numa mesma equação dois conceitos diferentes, mas que trazem o mesmo resultado:
$$\nabla \times \vec{B} = \mu _0 \vec{J} + \mu _0 \varepsilon _{0}{\frac {\partial \vec{E}}{\partial t}}$$
Vamos trocar os símbolos gregos pela língua portuguesa:
$$\textrm{campo magnético} = \textrm{corrente elétrica} + \textrm{variação do campo elétrico}$$
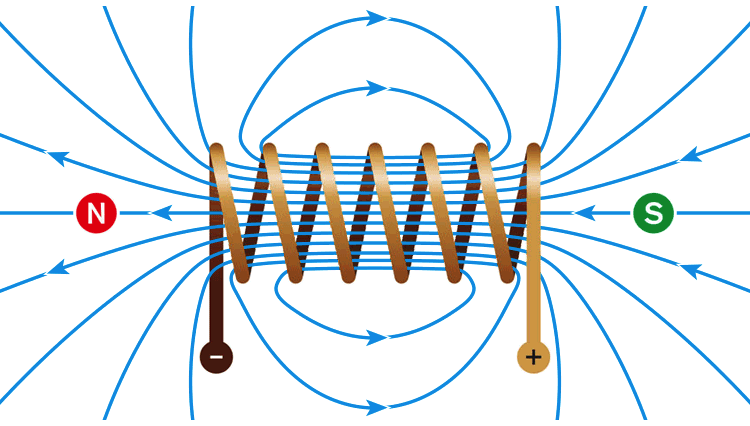
Olha como fica tudo muito mais fácil quando compreendemos o que a equação quer dizer. É simplesmente isso: um campo magnético pode ser criado por uma corrente elétrica, por uma variação do campo elétrico ou por ambos simultaneamente — por isso o sinal de adição. Também usamos esses objetos no dia a dia: eletroímãs ou solenoides (como os usados em HDs de computadores, alto-falantes, motores elétricos e carregadores sem-fio para celulares), geram o magnetismo a partir de correntes elétricas. Lembrando que a corrente elétrica precisa ser alternada, caso contrário não haverá campo magnético sendo produzido.
Você até pode se perguntar “onde foram parar os símbolos $\mu_0$ e $\varepsilon_0$?”. Eles continuam ali, fazem parte do cálculo da corrente elétrica e da variação do campo elétrico. Lembra que são constantes? Basta substituir os símbolos por aqueles números pré-definidos.
Comentei anteriormente que essa lei tem duas equações, inclusive tem o nome de duas pessoas. A primeira equação a surgir foi a Lei de Ampère, criada por André-Marie Ampère, a qual é somente a parte do $\mu_0 \vec{J}$, ou seja, corrente elétrica produz campo magnético. Porém, mais tarde, James Maxwell descobriu que uma variação no campo elétrico ($\frac {\partial \vec{E}}{\partial t}$) também produz os mesmos resultados, então Maxwell juntou tudo em uma única equação.
A velocidade da luz
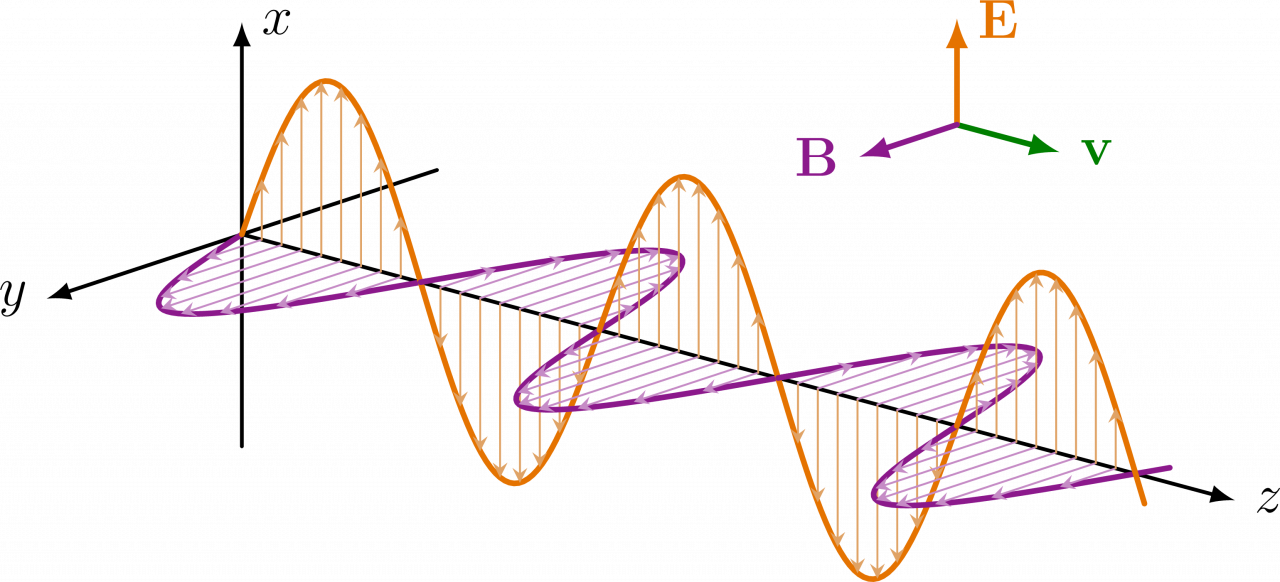
Em 1865, James C. Maxwell propôs que a luz era uma onda eletromagnética como qualquer outra e, portanto, deveria se propagar na mesma velocidade $c$ que foi encontrada na sua teoria do eletromagnetismo. Essa equação de onda eletromagnética é bem simples para tamanha importância:
$$c = \frac{1}{\sqrt{\varepsilon_0 \mu_0}}$$
O resultado será 299.792.458 m/s, a velocidade da luz no vácuo. Então, sim, a velocidade da luz é simplesmente o inverso da raiz daquelas duas constantes que mencionamos acima, as constantes elétrica e magnética. A constante elétrica pode ser chamada de permissividade do vácuo; e a constante magnética também é chamada de permeabilidade do vácuo.
Esse trabalho permitiu que Einstein pudesse trabalhar na sua Teoria da Relatividade Restrita e, futuramente, na teoria da velocidade da luz no espaço-tempo curvo.
Mas isso já é assunto para outra matéria.
Referências complementares
- FEYNMAN, R. P. Lições de Física: Edição do Novo Milênio. 2ª Edição. Porto Alegre: Editora Bookman. 2019.
- HALLIDAY, D.; RESNICK, R. Fundamentos de Física: Eletromagnetismo. Volume 3. 10ª Edição. Rio de Janeiro: Editora LTC. 2016.
- HEWITT, P. G. Física Conceitual. 12ª Edição. Porto Alegre: Editora Bookman. 2015.