A luz é composta de fótons, então poderíamos perguntar se o fóton tem massa. A resposta é definitivamente “não”: o fóton é uma partícula sem massa.
Segundo a teoria quântica moderna, um fóton tem energia e momento, mas não tem massa, e isso é mais do que comprovado. Mesmo antes de se saber que a luz é composta de fótons, já se sabia que a luz carrega momento e exercerá pressão sobre uma superfície. Mas isso não é evidência de que ela tem massa, pois o momento pode existir sem massa — a luz carrega momento na forma de energia.
Pode acontecer a interpretação de que o fóton tem massa porque tem energia e energia é equivalente à massa conforme a famosa fórmula de Einstein, $E=mc^2$. No entanto, muita atenção para o m em $E=mc^2$, pois nessa equação estamos falando de outro tipo de massa chamado massa relativística, um conceito da teoria da relatividade restrita que pode causar bastante confusão.
A massa relativística é uma medida da energia de uma partícula, que aumenta com a velocidade. A equação completa da relação massa-energia de Einstein também leva em conta o momento (p):
$$E^2=(mc^2)^2 (pc)^2$$
Por convenção, a massa relativística não é chamada simplesmente de “massa” na física contemporânea, portanto é errado dizer que o fóton tem massa dessa maneira. Você pode dizer que o fóton tem “massa relativística” se realmente quiser, mas não “massa”. Na terminologia atual, a massa de um objeto é sua massa de repouso, ou massa invariante, que medimos em quilogramas e que definitivamente é zero para um fóton.
Massa relativística vs. massa de repouso
Parte dessa discussão está preocupada apenas com a semântica, o significado dos termos. Pode-se pensar que seria melhor considerar a massa dos fótons como sua massa relativística (diferente de zero), ao invés da sua massa de repouso (zero). No entanto, o uso cotidiano define “massa” como sendo a massa de repouso de um objeto, principalmente porque a massa de repouso é mais útil ao fazer qualquer tipo de medição ou cálculo.

Massa relativística é equivalente à energia, razão pela qual massa relativística não é um termo comumente usado no cotidiano. Na visão moderna, “massa” não é equivalente à energia; massa é apenas a massa de repouso, aquela parte da energia de um corpo que não é energia cinética. A massa de repouso é independente da velocidade, mas a energia não. Portanto, é da massa relativística que estamos falando quando mencionamos na teoria da relatividade que ao se aproximar da velocidade da luz um objeto tende a “ganhar massa infinita”.
A massa relativística (M) é relacionada com a massa de repouso ($m_0$) da seguinte forma:
$$M = \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}$$
sendo v a velocidade do corpo que você está medindo.
Se o corpo não está se movendo, então a massa de repouso e a massa de relativística são iguais. No entanto, quanto mais rápido o corpo está se movendo, mais ele ganha massa relativística.
Belíssimo, não é?
Se não tem massa, por que a gravidade afeta a luz?
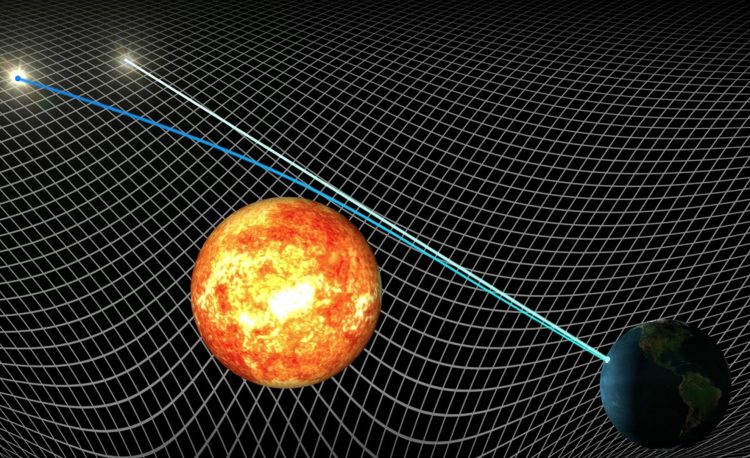
Enquanto escrevia esta matéria, vi uma postagem em uma rede social: “Se a luz não tem massa, como pode ser desviada pela gravidade de uma estrela?”.
A deflexão da luz das estrelas pelo Sol foi medida pela primeira vez por Arthur Eddington, no eclipse solar de 1919 que aconteceu em Sobral, no interior do Ceará, aqui no Brasil. O resultado foi consistente com as previsões da relatividade geral e inconsistente com a teoria newtoniana. Uma resposta para essa pergunta é que todas as partículas, incluindo os fótons, se movem de acordo com a relatividade geral e o caminho que seguem pelo espaço-tempo distorcido é independente de sua massa.
A gravidade distorce o próprio espaço, e tudo o que há nele terá seu caminho desviado. incluindo a luz.