As estrelas se mantêm estáveis devido à pressão das reações nucleares em seu interior se equilibrando com a força gravitacional gerada por sua massa. Todo o processo de evolução estelar se sustenta por essa regra. Por se tratar de um fluido, esse plasma em equilíbrio em uma estrela recebe o nome de equilíbrio hidrostático. Quando esse equilíbrio é interrompido a estrela busca uma nova forma de reencontrar esse balanço: o núcleo se encolhe, a temperatura aumenta e a fusão de elementos mais pesados é disparada. Mas temos um problema, anãs brancas não fundem matéria! Não há nenhuma reação nuclear acontecendo em seu interior para contrabalancear a intensa força gravitacional de uma anã branca ou de uma estrela de nêutrons. Como isso é possível?
Ao buscar entender como as anãs brancas e estrelas de nêutrons permanecem estáveis sem nenhuma pressão evidente do lado de dentro, nos depararemos com dois termos que são cruciais para se entender os remanescentes estelares: a matéria degenerada e o limite de Chandrasekhar.
Matéria degenerada?
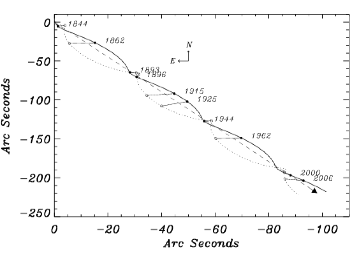
A história toda começa em 1834, quando o astrônomo e matemático alemão Friedrich W. Bessel, observando Sirius, descobriu que essa estrela tinha um movimento oscilatório irregular. Bessel concluiu, então, que Sirius deveria ter uma companheira invisível ao seu redor. Não foi até 1862, usando o maior telescópio refrator do mundo, que sua companheira fantasmagórica foi observada por Alvan G. Clark, estimando que essa estrela menor deveria ter uma massa comparável a do Sol, mas com uma luminosidade de 1/400 da nossa estrela. Essa estrela menor foi batizada de Sirius B. Na época, havia duas hipóteses: sua temperatura era muito baixa e, portanto, sua luminosidade também; ou Sirius B era uma estrela muito, muito pequena.
As coisas se tornaram ainda mais complicadas quando Walter S. Adams, astrônomo americano especializado nos estudos de espectrografia, coletou um espectrograma de Sirius B e viu que, na verdade, as linhas de absorção de Sirius B eram bem similares à de Sirius A. Como as estrelas irradiam determinados espectros de acordo com sua temperatura, então Sirius B não poderia ser uma estrela fria. Logo, a alternativa restante era que Sirius B deveria ser uma estrela quente, pequena e extremamente densa, sendo batizada então de “anã branca”.

Em 1924, nove anos depois, Arthur Eddington, um renomado físico e matemático inglês (também responsável pela observação do eclipse solar de Sobral, no Brasil, em 1919, que provaria a teoria da relatividade de Einstein) estipulou que se Sirius B realmente era tão densa como afirmavam, então, de acordo com a teoria da relatividade geral, o espectro da luz de Sirius B sofreria um desvio para o vermelho ao escapar de seu forte campo gravitacional. Eddington contatou Walter Adams e o pediu para medir esse desvio. No ano seguinte, Adams publicou suas descobertas, com os desvios para o vermelho confirmando que Sirius B era realmente uma anã branca extremamente densa. Sobre a descoberta, Eddington afirmou:
“O professor Adams matou dois pássaros com uma única pedra: ele fez um experimento comprovando, novamente, a teoria da relatividade geral de Einstein, e ainda confirmou nossas suspeitas de que matéria 2 mil vezes mais densa que platina não é apenas possível, mas está presente no nosso universo.”
WALI, K. C. Physics Today. Outubro de 1982, p.34
De acordo com Eddington, uma matéria de alta densidade com a compressibilidade de um gás perfeito é possível se, e somente se, a temperatura no interior dessa estrela for alta o suficiente para ionizar completamente os átomos, porque átomos ionizados, com seus núcleos e elétrons livres, formam um agregado diferente dos átomos encontrados na Terra. Essa matéria teria partículas livres milhões de vezes menores do que os átomos compostos e, portanto, poderiam ser comprimidos em volumes muito menores. Essa redução de tamanho tornaria uma matéria exótica extremamente densa plenamente possível.
Mas… como?
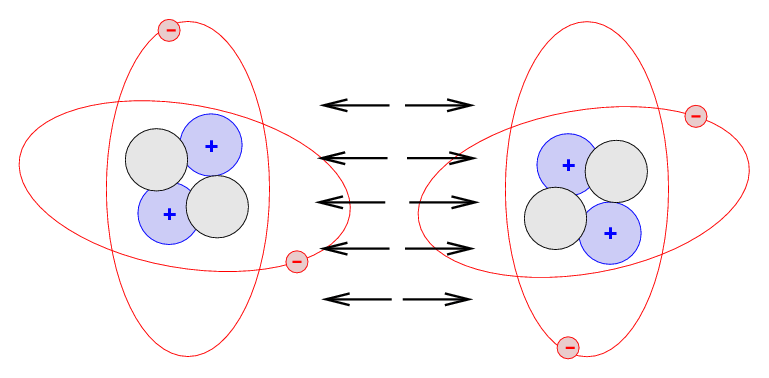
Durante as aulas de física e química na escola aprendemos que existem três estados físicos da matéria: sólido, líquido e gasoso. Nesses três estados, a matéria é composta por átomos, que formam moléculas, e que se repelem mutuamente devido às interações eletromagnéticas envolvidas: elétrons têm cargas negativas, logo, cargas iguais têm a tendência de se repelir. Por isso dois átomos fora de ligações moleculares nunca podem se tocar. Nós nunca, de fato, tocamos as coisas, o que sentimos é a repulsão gerada pelas forças eletromagnéticas.
Ainda durante o colégio podemos estudar sobre um quarto estado da matéria, o plasma. Falamos bastante sobre ele na nossa série sobre evolução estelar, o plasma se consiste em prótons e elétrons livres. Não há átomos em ligações moleculares, apenas férmions se movimentando livremente com alta energia cinética. Normalmente — mas não é regra — essa energia cinética é alimentada pelo calor, por isso as estrelas são feitas de plasma. No entanto, existem mais estados da matéria além desses quatro que podem ocorrer naturalmente, e um deles é muito importante no estudo de remanescentes estelares: a matéria degenerada.
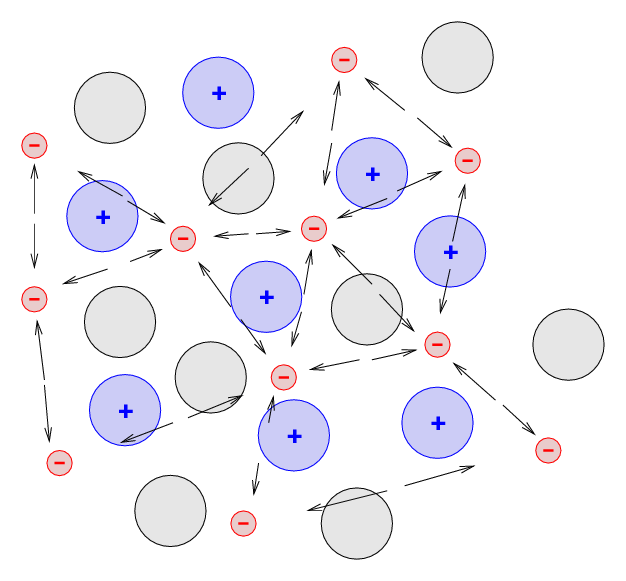
A matéria degenerada se assemelha ao plasma pois também é composta por partículas livres, mas com uma enorme diferença: enquanto o plasma é composto de partículas se movimentando livremente com alta energia, a matéria degenerada é um sistema de partículas compactadas em altíssima densidade.
Em um átomo, os elétrons podem trocar de níveis e serem ionizados, perder ou adquirir elétrons, mas em sistemas com densidade extremamente alta — como em uma anã branca — os átomos deixam de existir e a matéria não pode mais ser comprimida. Não há mais espaços vazios consideráveis entre as partículas e o gás começa a se comportar quase como um sólido. Esse sistema de altíssima densidade de matéria fermiônica adquire propriedades físicas bem peculiares e esse estado físico recebe o nome de matéria degenerada.
Essa matéria se sustenta e evita seu próprio colapso porque quando essas partículas são submetidas à pressões extremas, são as leis da mecânica quântica, e não da física clássica, que começam a predominar nesse sistema.
O princípio de exclusão de Pauli
Um dos conceitos mais fundamentais no estudo da matéria degenerada e do porquê de ela existir é o princípio de exclusão de Pauli. Ele descreve que não mais que dois férmions podem ocupar o mesmo estado quântico — por exemplo, dois elétrons, um spin up e um spin down. Um átomo de hidrogênio tem apenas um elétron no nível 1s, que pode ser um spin up, por exemplo. Um átomo de hélio tem dois elétrons no nível 1s (configuração designada como $1s^2$), se um é spin up o outro deve, obrigatoriamente, ser spin down.

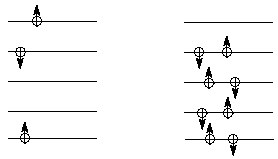
Um átomo de lítio possui três elétrons, dois deles (um spin up e outro spin down) estão juntos no primeiro orbital 1s no primeiro subnível. O terceiro elétron se localiza em um orbital eletrônico diferente dos outros dois, chamado de 2s, localizado sozinho no segundo subnível. Cada orbital atômico comporta apenas dois elétrons, cada um com propriedades quânticas diferentes. Observe no diagrama anterior como os elétrons são distribuídos e preenchem os orbitais atômicos nos átomos de carbono (C) e enxofre (S).
É devido a esse princípio, o princípio de exclusão de Pauli, que elétrons resistem bravamente à compressão. Em um gás convencional, os elétrons podem transitar de camadas livremente. Mas na matéria degenerada, os elétrons já ocupam todos os subníveis possíveis. Uma estrela extremamente densa, como uma anã branca, com gravidade em níveis extremos, ainda consegue se sustentar porque existe uma força que impede que os elétrons invadam os subníveis alheios já preenchidos. Essa força que resiste à compressão se chama pressão de degenerescência eletrônica.
Portanto, em estrelas compostas de matéria degenerada — não apenas as anãs brancas, mas também estrelas de nêutrons —, a pressão que mantém a matéria em equilíbrio não é mais da energia térmica ou eletrostática, mas proveniente dos princípios mais profundos da mecânica quântica.
O limite de Chandrasekhar

A equação leva o nome do astrofísico indiano Subrahmanyan Chandrasekhar, que foi laureado com o Nobel de Física de 1983 ao demonstrar como a mecânica quântica e a mecânica estatística se associa com a evolução das estrelas.
Como acabamos de ver, a pressão de degenerescência eletrônica é a força que impede que dois elétrons idênticos ocupem o mesmo estado quântico. É essa a força interna que mantém uma anã branca estável, apesar de sua intensa força gravitacional. No entanto, como tudo na natureza, sempre existe um limite onde essa força se rompe. Quanto mais densa uma estrela anã branca se torna, mais rápido os elétrons se movem. Eventualmente, os elétrons estão se movendo perto da velocidade da luz; eles não podem ir mais rápido do que isso, portanto há um limite para a intensidade da pressão de degeneração. Para uma anã branca, o limite para essa pressão se sustentar tem um valor: 1,44 massas solares. Se uma anã branca excede 1,44 massas solares, a força gravitacional é tão intensa que a pressão de degenerescência dos elétrons não é mais suficiente para mantê-los em seus respectivos níveis. Os elétrons, então, vencem sua repulsão mútua e são empurrados ainda mais para dentro, combinando prótons e elétrons, formando nêutrons — e liberando uma enxurrada de neutrinos no processo. O resultado é o que chamamos de estrela de nêutrons.
Esse limite máximo de 1,44 massas solares até onde uma anã branca permanece estável se chama limite de Chandrasekhar e, matematicamente, a fórmula se parece com isso:
$$M_{limit} = \frac{\omega^0_3 \sqrt{3\pi}}{2} \left(\frac{\hbar c}{G}\right)^{\frac{3}{2}} \frac{1}{(\mu_e m_H)^2}$$
Onde $\hbar$ é a constante reduzida de Planck, $c$ é a velocidade da luz, $G$ é a constante gravitacional, $m_H$ é a massa do átomo de hidrogênio, $\mu_e$ é a massa molecular média por elétron (que depende da composição da estrela) e $\omega^0_3$ é uma constante matemática com valor aproximado de 2,018236.
O limite de Chandrasekhar não é apenas o limite superior para a massa máxima de uma anã branca, mas também um limiar. Um núcleo de estrela que ultrapassa esse limiar não guarda mais sua preciosa carga rica em elementos pesados. Em vez disso, ela as entrega ao Universo como um todo em uma supernova que marca sua própria morte, mas torna possível a existência de vida.