Apesar de a relatividade restrita cair como uma luva para as leis que governam a mecânica, a eletricidade e o magnetismo, a peça faltante ainda era a gravidade. Foi pensando nisso que Einstein percebeu a sutil conexão entre a aceleração e a gravitação.
O princípio da equivalência
Ele imaginou que uma pessoa dentro de um elevador não conseguiria distinguir se ela está parada na superfície da Terra com uma aceleração gravitacional de 1 G (9,81 m/s2) ou em um foguete acelerando pelo espaço a 9,81 m/s2. Da mesma forma, também não haveria diferença entre uma pessoa em queda livre ou em gravidade zero — uma pessoa em queda livre se sentiria sem peso algum, como se a gravidade deixasse de existir.
Essas ideias simples, chamadas de princípio da equivalência, foram a base para Einstein perceber que a queda livre também era um movimento inercial e, portanto, as leis da relatividade também deveriam se aplicar.

Einstein percebeu que a gravidade tem a propriedade, e é a única força com essa propriedade, de desaparecer como resultado de seu próprio efeito. Se estivéssemos em queda livre por causa da gravidade e sem a resistência do ar, nós nos sentiríamos sem gravidade. Soa contraditório, mas é assim que os aviões que simulam gravidade zero funcionam: despencando das alturas, mas de forma controlada — do contrário seria o último passeio de todos.
Pensando dessa forma, um sistema de referência não-inercial (acelerado) é exatamente igual à força gravitacional em um sistema inercial (em repouso), logo, a gravidade também deveria se aplicar de algum modo dentro da relatividade. Mas a Terra é redonda, não há como ter uma “aceleração para cima” em todos os lados do planeta, portanto, a única resposta seria que a própria geometria do espaço-tempo seria curva.
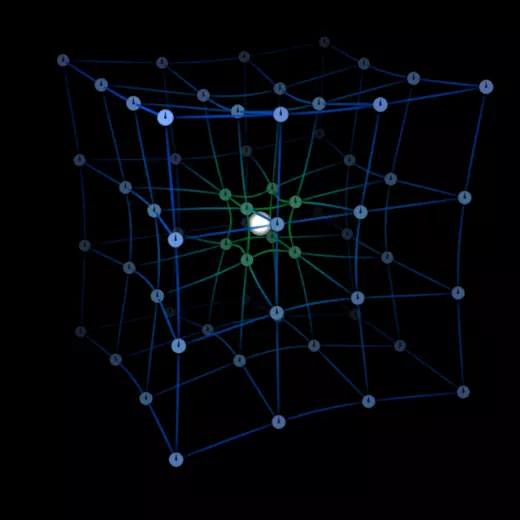
Apesar do espaço ser tridimensional, podemos imaginar a gravidade de Einstein como um tecido de borracha. Objetos pesados criam uma deformação nesse tecido, atraindo tudo ao seu redor. Quanto mais pesado o objeto, maior a curvatura gerada.
Tendo formulado sua visão relativística da gravidade, uma questão ainda permanecia: para Newton, gravitação era uma característica da massa, mas qual seria a origem da gravidade na relatividade geral?
Einstein publicou em 1913 que a razão para o espaço-tempo se curvar é a combinação de energia e momento, levando-o a intensos estudos sobre espaços e superfícies curvas nos trabalhos desenvolvidos pelo matemático George F. Riemann, chamado de geometria riemanniana. Apesar de, inicialmente, Einstein não ter encontrado as equações que relacionassem massa, energia e momento com a curvatura do espaço, com a ajuda de amigos matemáticos essas equações foram finalmente desenvolvidas e publicadas em novembro de 1915. Essa teoria passaria a se chamar teoria da relatividade geral, dando origem à equação de campo de Einstein:
$$G_{\mu\nu} \equiv R_{\mu\nu} – \frac{1}{2}R g_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu}$$
Essa é, sem dúvida, a equação mais importante da relatividade geral, que alterou para sempre a nossa percepção do Universo. No lado direito da fórmula, o elemento $G_{\mu\nu}$ é o tensor de Einstein, seguido por uma série de outras constantes e tensores, como o tensor de curvatura de Riemann. Envolveria uma dose cavalar de matemática avançada para explicar esses pontos, mas basta dizer que a solução encontrada por Einstein foi brilhante, não à toa um dos maiores físicos de nossa história.
Validando a relatividade geral
Antes mesmo de sua publicação final em 1915, uma expedição científica para validar a relatividade geral já havia sido feita um ano antes, em 1914, com equipes na Alemanha, na Argentina e nos EUA para observar um eclipse solar. A questão era: se Einstein estivesse realmente certo e a curvatura do espaço fosse verdadeira, a gravidade do Sol iria desviar ligeiramente o caminho da luz das estrelas próximas. Com a Lua cobrindo a intensa luz do Sol, as estrelas ficariam visíveis para serem fotografadas.
Mas, com o início da Primeira Guerra Mundial, a expedição alemã foi detida e presa. Apesar das equipes na Argentina e nos EUA não terem sido detidas, o tempo nublado prejudicou a observação do eclipse solar nesses locais e, portanto, foram incapazes de concluir a pesquisa.
Esse foi um acaso de muita sorte para Einstein, pois, nesse ano de 1914, suas equações de campo ainda estavam incompletas e, consequentemente, incorretas. Se o eclipse solar tivesse sido observado, os resultados experimentais obtidos seriam discrepantes com as previsões teóricas, o que invalidaria a teoria da relatividade e prejudicaria a credibilidade de Einstein. Em 1915, Einstein corrigiu todas as suas equações antes da publicação final de seu trabalho.

Em 1919 a teoria da relatividade foi colocada novamente à prova. Foi realizada uma nova expedição com o astrônomo britânico Arthur Eddington para onde aconteceria um novo eclipse solar total. Novamente, o céu claro e a Lua cobrindo completamente o disco solar permitiria que as estrelas da constelação de Touro fossem fotografadas e analisadas. Parte da expedição rumou para a ilha de Príncipe, na costa da África, e outra para a cidade de Sobral, aqui no Brasil, para fotografar o eclipse solar, comparar a posição das estrelas e verificar se os desvios eram compatíveis com a relatividade geral. O resultado foi que sim, eles eram. As posições das estrelas estavam ligeiramente deslocadas devido à gravidade do Sol, exatamente nas mesmas medidas de ângulo previstas pelas equações da relatividade geral de Einstein.
O sucesso das previsões e das observações do eclipse de 1919, validando a relatividade geral, estamparam a capa dos jornais na época, tornando Einstein e sua teoria mundialmente famosos.
Apesar do ceticismo com relação aos erros instrumentais dos equipamentos rudimentares e de suspeitas de viés de confirmação, Einstein passou por mais um experimentum crucis em 1923, quando o astrônomo William Campbell divulgou resultados prévios das medidas com alto rigor científico de mais de 3.000 estrelas. Todos os resultados validaram novamente a teoria da relatividade geral.