Em termos da gravidade, podemos definir a atração entre dois corpos com massa (como um planeta orbitando uma estrela) por meio da lei da gravitação universal de Newton. Essa lei nos diz que dois corpos com massa ($m_1$ e $m_2$) geram uma força de atração inversamente proporcional ao quadrado da distância entre eles ($r^2$), tudo isso proporcional a uma constante gravitacional ($G$), ou seja:
$$F = G \frac{m_1 m_2}{r^2}$$
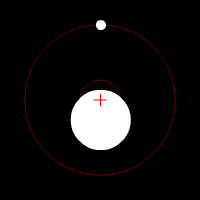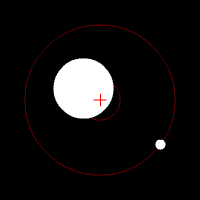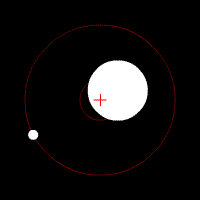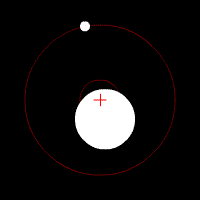
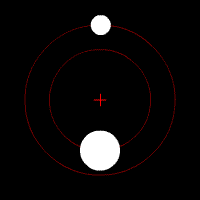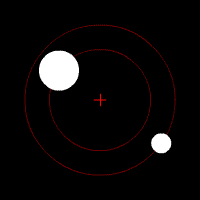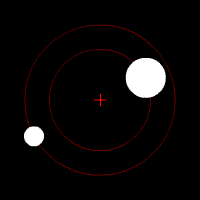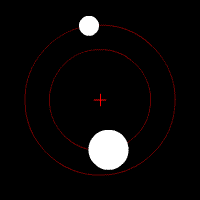
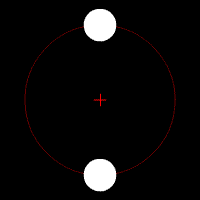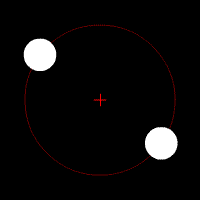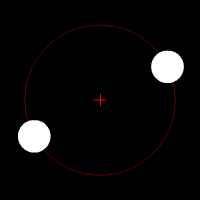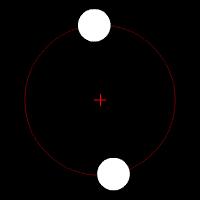
Essa equação simples consegue descrever a órbita da Lua ou da Estação Espacial Internacional ao redor da Terra, a órbita da Terra ao redor do Sol, duas estrelas em um sistema binário, uma estrela orbitando um buraco negro, ou de qualquer problema envolvendo dois corpos. Essas órbitas são previsíveis e estáveis, pois um corpo atrai o outro, como dois dançarinos numa pista.
NOTA: Aqui não precisamos da relatividade geral, pois não estamos lidando com situações em escala cosmológica ou que envolva cenários relativísticos.
O problema acontece quando adicionamos um terceiro corpo nesse sistema. Esse terceiro corpo perturba a órbita dos outros dois corpos, atraindo-os. Essa perturbação também afeta a órbita dos dois primeiros corpos, que também afetará a órbita do terceiro, e assim por diante. Essa reação em cadeia produz um sistema caótico.
Assim como acontece com a turbulência de um fluido, não há nenhuma solução fechada na física capaz de prever um sistema de três corpos, pois eles se mostram completamente aleatórios. Esse é o problema dos três corpos.
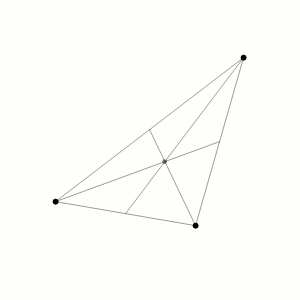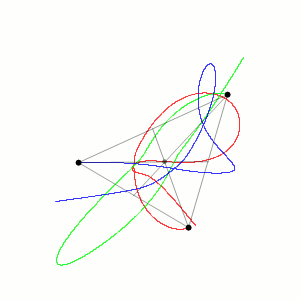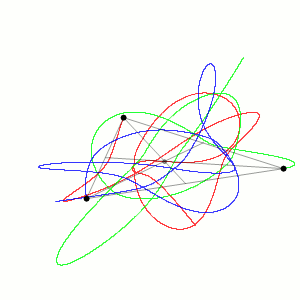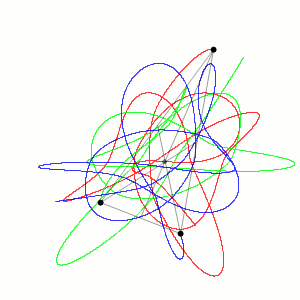
A complexidade do problema dos três corpos surge do fato de que pequenas variações nas posições iniciais ou velocidades dos corpos podem resultar em trajetórias muito diferentes com o passar do tempo. Como a força exercida pela gravidade entre os corpos depende da posição e da distância entre eles, e essas posições e distâncias variam continuamente, uma descrição matemática só é possível por meio de equações diferenciais ordinárias não-lineares de segunda ordem.
Essas equações não são fórmulas prontas que nos dão a posição final dos corpos (como costuma acontecer nas fórmulas de aceleração e velocidade que vemos na física), e sim permitem determinar a progressão passo-a-passo de um sistema caótico a medida que o tempo vai passando.
Um exemplo de uma dessas equações para o corpo 1:
$$\frac{d^2\vec{r_1}}{dt^2} = G \left( \frac{m_2}{|\vec{r_1}-\vec{r_2}|^3} (\vec{r_2}-\vec{r_1}) + \frac{m_3}{|\vec{r_1}-\vec{r_3}|^3} (\vec{r_3}-\vec{r_1}) \right)$$
E essas equações precisam ser resolvidas também para o corpo 2 e o corpo 3. Isso nos dá um “mapa” do que está acontecendo com os três corpos (como a direção e a intensidade das forças), de quem está atraindo quem, em um instante de tempo. Para outro instante de tempo, as equações devem ser recalculadas, pois a posição dos corpos mudou — e as forças também mudaram.
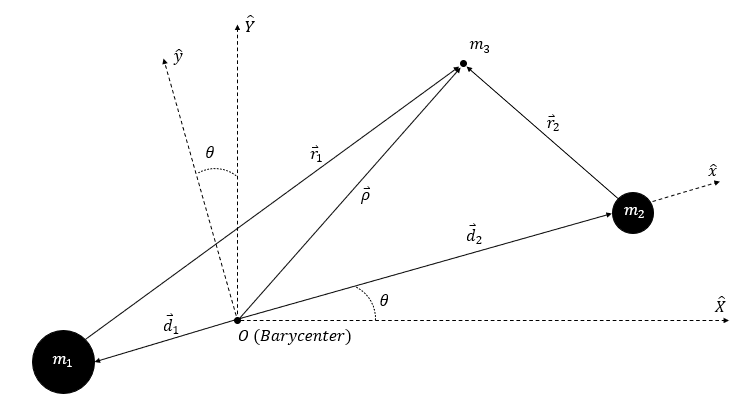
Estas simulações podem fornecer previsões altamente precisas das posições dos corpos ao longo do tempo, mas não oferecem uma fórmula direta para descrever o movimento para todas as condições iniciais.